CodinGame Fall Challenge 2020 参加記
お久しぶりです。
CodinGame Fall Challenge 2020 に参加したので参加記を書きます。もう眠いです。。。
注意
「自分でもなんで強いかわからない」みたいな改善案ばかりなので、多くの方の役に立たない可能性が高いです。
あと普通に間違ってる可能性も高いです。優しさに自信がある方はご指摘ください。
こんなことしてる人もいるんだなぁ、ぐらいの気持ちで読んでいただけると嬉しいです。
ルール
ツカモさんに全てを託します(ありがとうございます) tsukammo.hatenablog.com
ざっくりボドゲっぽくいうと、
デッキ構築 + セットコレクション + (拡大再生産)かな、という感じです。
ボドゲっぽく言わないと、いい感じに素材の交換を繰り返して決められたセット(ポーション)を作っていこう、という感じです。
結果
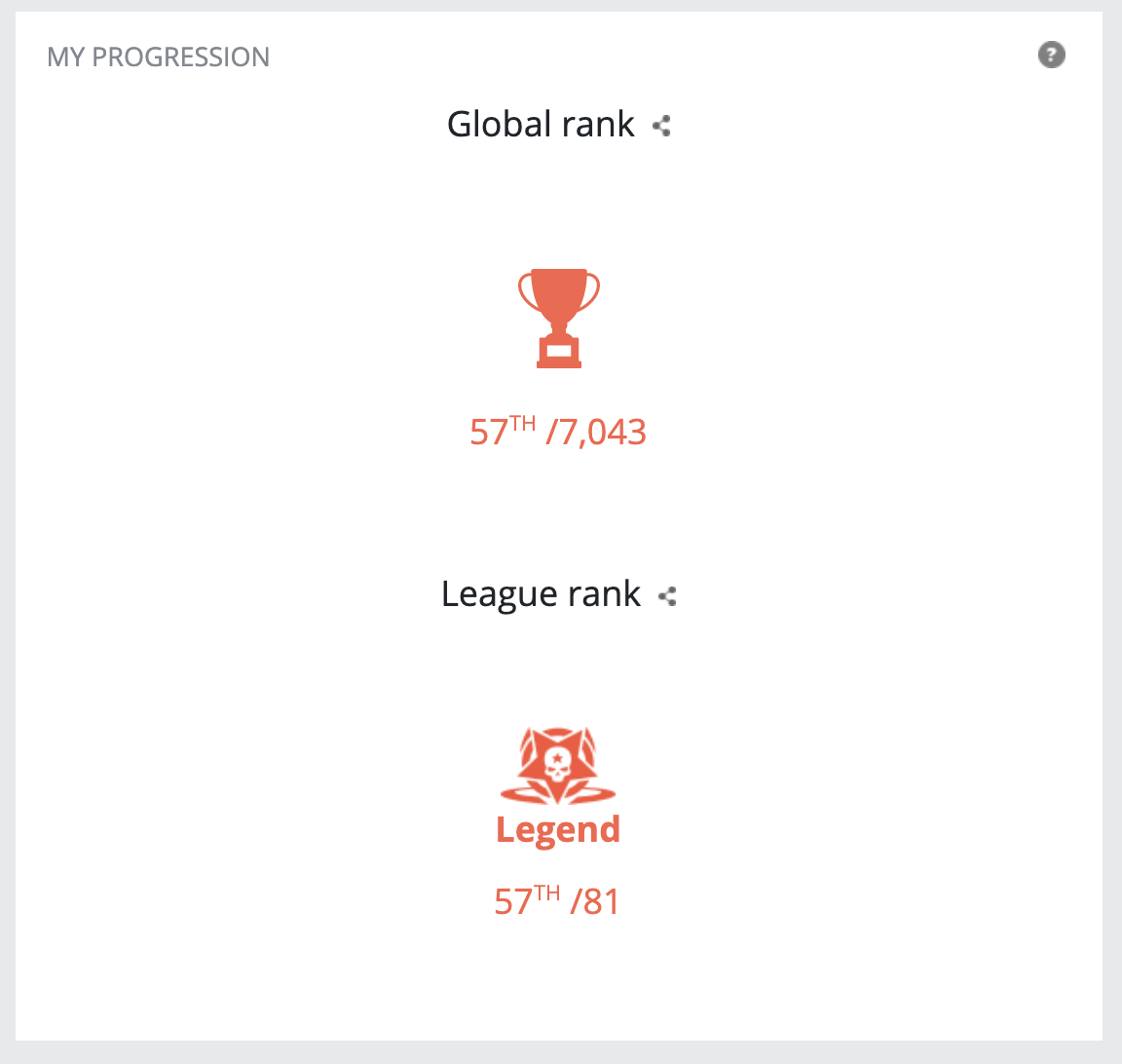 世界 57位 / 7043人(日本 14位 / 320人)で、Legendでした。
世界 57位 / 7043人(日本 14位 / 320人)で、Legendでした。
終了3時間前にギリギリレジェンドに上がりまして、最終提出も結局そのコードを出したのですが思ったより上に行けたのは嬉しい誤算でした。
やったこと
やったことを書きます。
つらつらと箇条書きです。
各Tierの価値について
探索について
- 幅75、深さ25のビームサーチを行いました。
- 探索内容は、各ターンでできるムーブを全て試す、です。(LEARNについては少し違うので後述します)
- ただし、現在のターンに自分が取れずに相手が取れるポーションについては考慮から外しました。
本当は安いポーションを相手がとるとは限らないから、そこも考慮した方がいいらしいです。
「実は先にRESTする方が強い」「実は先にLEARNする方が強い」みたいなのを取りこぼしたくなかったので、 3手目までは全探索することにしました。
- 最初はビームサーチで書いていて、途中でchokudaiサーチに切り替えたのですが、思うように順位が上がらず、最終日にビームサーチに戻したら順位が爆上がりしました。
- たぶんどこか壊れてます(chokudaiサーチもgold30位とかに入ってたから特別弱い訳ではないと思うんですが)
評価値について
- 5つ目のポーションを取得するまでは、 (インベントリのTier価値総和 + 獲得したポーションの点数)の、探索前からの伸びを探索ターン数で割ったものを評価値としました。
- 25手目のRESTについては分母に入れてはかわいそうなので、無視することにしました。
- 「インベントリの価値を高め続けるよりも、途中でポーション作ったほうが点が高くなるよ」とおばあちゃんに教えてあげました。
- が、準トライフォース職人おばあちゃんになってしまいました。
- ので、ポーションの価値を一律 +7しました。 (は?)
するとなんかいい感じにバランス高い動きをするようになりました。(えらいぞ)
ポーション価値をターンに応じて減衰させようとは思ったのですが、インベントリ価値が相対的に高くなって壊れそうなのでやりませんでした。
6手目はとにかく速くポーションを作るようにしました。超大事だと思ったんですが、そこまで伸びませんでした。
- 6つ目のポーションで相手より9点リードしている場合に限り、速さを重視するようにしたら強くなりました。
- なんとなく、「どうせ相手はこの数ターンで点を伸ばすから〜」の気持ちでした。
- ターン開始時に5つポーションを取ってないと速さを重視しないバグがあったのですが、外すと弱くなったのでそのままにしました。
25手とか読むと多分皮算用色が強くなるのかなと思ったり。 (というか25手先の状況って妥当な推測ができるのかといまだに思ってます)
振り返ると激ヤバ関数ですが、激ヤバ探索にはfitしたのでヨシ!
LEARNについて
- 初手7回一番下からLEARN。それに加え、先読み税3以下のものを最大3つまで、後の探索で取得できるようにしました。
- いい詰み回避になったと思いましたが、実は初手6手で良かった説が高いです。だって後の探索を最大4回にすればほとんど変わらないもの。
- 各探索におけるLEARNは最大1回までとしました。状態数がぐっと減ってより幅を持たせられるようになった気がします。
呪文について
- 特に評価はつけてません。
- 下7回が普通にSilverまで強かったのと、最大3回の追加LEARNでそこそこまとまるだろうと考えました。
- 初手の青+2 以外の呪文は禁止しました。
その他
- トライフォースは5個までしか価値がないようにしました(集めすぎるの回避)
- 勝てる時はキッチリ勝つようにしました。
- 相手が6つ目のポーションを作れる時には、得点を最大化するようにしました。(たとえ勝っている時でも!)
- 普通に考えたら無駄に負ける可能性が上がるバグなんですが、上位陣で勝戦判定をやってない人はほぼいないでしょうし、いい感じに混乱をうんだのかもしれません。
振り返り
- SpringChallenge2020が大苦戦したことに比べれば、中盤までは比較的高い順位をキープしながら楽しめました。
Legendが解放されてからは、案の定?大苦戦しました。
SilverまではPython、Gold解放後は11月からこっそり勉強していたRustに乗り換えました。
- お受験ママみたいなコンパイラに叱られ続けてつらかったです。
Rust移行も大苦戦しましたが、最終日にはそれなりに慣れれてよかったなと思います。
初めてビームサーチとchokudaiサーチを書きました。
- 後者は実は壊れてたかもしれませんが、新しいことずくめの中でなんだかんだ結果を出せて嬉しく思います。
生活の破壊について
- 木金と有休を使って怒涛の5連休を作り出しました。
- 平均して平日は1日3時間、休日は14時間近くやったと思います。
- 最後の2日ぐらいはご飯も食べずにずっとやってました。
- 生活を破壊するのはやめよう!
- やめような!!!
まとめ
振り返ってみれば春に負けず劣らず、苦戦したコンテストでしたがいい結果が出てほっとしています。
特に全力を出した感については春よりも大きいかな。。。
対戦してくださった方々、ここまで読んでくださった方々、ありがとうございました! CodinGame Spring Challenge 2021 でお会いしましょう!!!
Donutsプロコンチャレンジ2015 C - 行列のできるドーナツ屋
問題原文
解法
人 について考えている時、
- いま見えている人の数を
の答えとする
- いま見えている人のうしろから見て行って、
より小さいものは今後見えなくなるので削除
を今見えている人として末尾に追加
で解ける。
これはスタックを使うと楽に実現できる。
本質的には、
と同じにみえる。
実装
番兵を先に積んでおくと楽です。
N = int(input()) H = list(map(int, input().split())) ans = [-1] * N stack = [float('inf')] for i, h in enumerate(H): ans[i] = len(stack) - 1 while stack[-1] < h: stack.pop() stack.append(h) print(*ans, sep='\n')
感想
このテクニック、いい。(特に平衡二分木が標準で備わってない言語は)
ABC170 D - Not Divisible
問題原文
解法
エラトステネスの篩っぽく、「 を割るような
が何個あるか」を数える。
これは調和級数っぽい形になるので、実は ぐらいでできる。
ただし重複する数をそのまま処理すると、2 2 2 2 .... 2 2 2 をはじめとするパターンでTLEしてしまうので注意。
実装
ほんとは から回すべきだった。
それなら boolで判定できるので。
from collections import Counter N = int(input()) A = list(map(int, input().split())) C = Counter(A) A = set(A) MAX_A = 10 ** 6 X = [0] * (MAX_A + 1) for a in A: for i in range(a, MAX_A + 1, a): X[i] += 1 ans = len([a for a in A if (X[a] == 1) and (C[a] == 1)]) print(ans)
感想
篩の考え方しょっちゅうでるなぁ。
ABC172 D - Sum of Divisors
問題原文
解法
普通に解けなかったので解説をガン見した。
キーとなる性質は「ある数 が 何かで割れると、答えが
される」ということ。
で、例えば は当然どれも 5で割れるわけなんですが、これは答えに
されるのと同じ。
つまり、等差数列の和の公式で一発で出せますね。。。
これを についてやればOK
。
で通る。
実装
N = int(input()) ans = 0 for x in range(1, N + 1): n = N // x ans += n * (2 * x + (n - 1) * x) // 2 print(ans)
感想
敗因は は切りわけにくそうと決め付けちゃったことかなぁ。。。 視点を切り替え切れませんでした。
こういうのかなり弱点そう。
ABC172 E - NEQ
問題原文
解法
まず全パターンは、 「 個の数から
個選んで並べる」を「
と
に対してやる」 ので、
通り。
ここから、ダメなパターンを引いていくことを考える。
ダメなパターンは「1つが一致しているパターン」「2つが一致しているパターン」「3つが。。。」の形になってるので、なんか包除原理が使えそうだなとなる。
考えるべきことは以下。
例えばここでは、 個一致しているパターンを考える。
個の数から
個選ぶ
個の置き場所から
個選んで並べる
- 残り
個から、
個選んで並べる。これを
,
に対してやる。
すると以下のようなコードになる。↓
実装
N, M = map(int, input().split()) MOD = 10 ** 9 + 7 factorial = [1, 1] inverse = [1, 1] invere_base = [0, 1] for i in range(2, N + M + 1): factorial.append((factorial[-1] * i) % MOD) invere_base.append((-invere_base[MOD % i] * (MOD // i)) % MOD) inverse.append((inverse[-1] * invere_base[-1]) % MOD) def nCr(n, r): if not (0 <= r <= n): return 0 return factorial[n] * inverse[r] * inverse[n - r] % MOD def nPr(n, r): if not (0 <= r <= n): return 0 return nCr(n, r) * factorial[r] % MOD ans = pow(nCr(M, N) * factorial[N], 2, MOD) for r in range(1, N + 1): p = nCr(M, r) * nPr(N, r) * pow(nPr(M - r, N - r), 2, MOD) % MOD p *= ((-1) ** ((r % 2) ^ 1)) ans -= p ans %= MOD print(ans)
感想
本番は の残りについての並べ方を考慮してなかった(なんで?????)
ちゃんと としてもっておきましょう。。。
ABC168 E - ∙ (Bullet)
問題原文
解法
実験とかすると、 は
としていいことは分かる。(一旦0は無視で)
これをとりあえず集計したくなる。
集計の結果、例えば が
個、
と仲が悪いものの個数が
個 ということがわかれば、
S からも Tからも選ばない S から1つ以上選ぶ T から 1つ以上選ぶ 通り数を足し合わせたものがそのキーに関しての通り数となって、答えが計算できそうということがわかる。
ただ、 と仲が悪いものは、
であったり、
であったりしてめんどくさい。
これは、片方がマイナスのものはマイナスを の方に押し付けることで、まとめて集計できる。
(たとえば、 は
として集計する)
また、 のようなものは
のようにしても問題ないので、そのようにして集計する。
のような片方0に関しては、 仲が悪いものは
のようなもう片方が0のものになる。
後々計算しやすくするように、 が 0なら
として、
が 0 なら
として集計しておく。
は他の全てと仲が悪いので、「
から1つ選ぶ」という組合せを完全に別で計算する必要がある。
これは普通に の数を数えておくことでできる。
実装
複雑ではないんだけどひ〜
from math import gcd from collections import defaultdict N = int(input()) MOD = 10 ** 9 + 7 zero_zero_num = 0 fishes = defaultdict(int) for i in range(N): a, b = map(int, input().split()) if a == 0 and b == 0: zero_zero_num += 1 elif a == 0: fishes[(0, -1)] += 1 elif b == 0: fishes[(1, 0)] += 1 else: g = gcd(a, b) a, b = a // g, b // g if (a > 0 and b > 0) or (a < 0 and b < 0): fishes[(abs(a), abs(b))] += 1 else: a, b = (-a, -b) if a < 0 else (a, b) fishes[(a, b)] += 1 ans = 1 keys = list(fishes.keys()) visited = set() for (kai, kbi) in keys: if kbi >= 0: kaj, kbj = kbi, -kai else: kaj, kbj = -kbi, kai if ((kai, kbi) in visited) or ((kaj, kbj) in visited): continue ans *= (1 + (pow(2, fishes[(kai, kbi)], MOD) - 1) + (pow(2, fishes[(kaj, kbj)], MOD) - 1)) ans %= MOD visited.add((kai, kbi)) visited.add((kaj, kbj)) print((ans + zero_zero_num - 1) % MOD)
感想
キーを集計しやすいようにあらかじめ変形する みたいなテク?なのかな。。。
bにマイナスを押し付けるとこんなに楽になるんだなぁ。勉強になりました。
CODE FESTIVAL 2014 予選B D - 登山家
問題原文
解法
ぱっと思い浮かぶのが、平衡二分探索木 + が大きいものから見て行って、すでに見たやつに対して二分探索。
とはいえ当方はPythonなので\(^o^)/になる。
ここから解説に載ってた別の解き方。
まず、「ある山小屋のより東であって高い位置にあるような最も西の山小屋」が求められればその逆も求められるので、片方向についてのみ求めることを考える。
キーとなる性質は、「山を東から見て行って、今見ている山小屋から見える山は一度見たら二度考える必要はない」ということ。
例えば、 5 3 3 3 とあって、 5 からは 3 3 3 が見えるが、一度見たらこれは二度考える必要がない。もう一つ西を見て、仮に 4 5 3 3 3 だった場合には 4 は 5 で止まるし、 6 5 3 3 3 だった場合、 6 からは 3 3 3 が見えることは確定している。
これを踏まえると以下のようなアルゴリズムで、「ある山小屋のより東であって高い位置にあるような最も西の山小屋」が求められる。
- スタックにこれまで見た山小屋を積んでいくことを考える
- 今見ている山小屋からスタック先頭の山小屋が見える限りpop
- 2を満たさなくなった時点でスタックの先頭にあるのが求めたい山小屋
- いま見た山小屋をスタックの先頭にpush
実装
なんとなく共通化したかった。
番兵をおくと楽です!
N = int(input()) H = [int(input()) for _ in range(N)] def calc(H): ret = [0] * N stack = [N] for i in reversed(range(N)): while H[stack[-1]] <= H[i]: stack.pop() ret[i] = stack[-1] - i - 1 stack.append(i) return ret ans_l = calc(H + [float('inf')]) ans_r = calc(H[::-1] + [float('inf')])[::-1] for al, ar in zip(ans_l, ans_r): print(al + ar)
感想
先にぱっと解法が見えて、それがどうやら実装困難なことがわかると思考が止まっちゃうな。。。
勉強になりました。
と同じ雰囲気を感じますね。 RMQ + 二分探索で殴れはしそう。