Python:Union-Find木について
どうもこんにちわ。AT274です。
今回は素集合データ構造であるUnion-Find木について学んだのでまとめてみました。記事後半にPythonでの実装例を載せています。
コードだけ見たい方は目次から完成形に飛んでくだされ。
Union-Find木の概要とイメージ
まずは、Union-Find木が何をどんな風に管理するのかざっくりまとめます。
素集合とは
Union-Find木は素集合を管理するデータ構造です。では素集合とは何でしょうか。Wiki先生によると、
一般に、与えられた集合族が互いに素(英語: pairwise disjoint)、あるいは素集合系(そしゅうごうけい、英語: disjoint sets)であるとは、その集合族に含まれるどの2つの集合をえらんでも、それらの選び方に依らずそれらが常に共通部分を持たないことをいう。
素集合 - Wikipediaより
とのことです。
ちょっと具体例を挙げて確認してみましょう。
ちょっと下の画像を見てみてください。
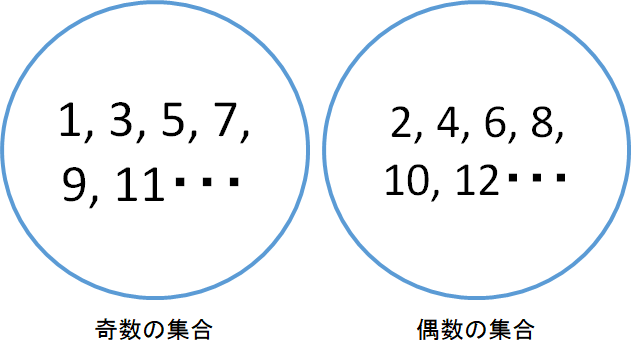
これらは互いに素な集合でしょうか?答えはYESです。
それでは、
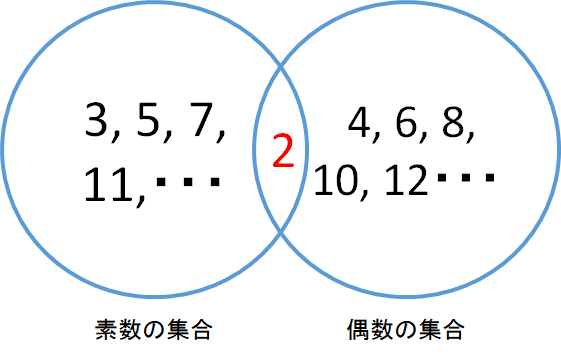
これらは互いに素な集合でしょうか?答えはNOです。
2が二つの集合の共通部分になってしまっていますね。
数学的には、A∩B = φ(空集合)ならばAとBは互いに素な集合ということになります。
Union-Find木のイメージ
さて、Union-Find木では上記のような集合系を木構造で管理します。
イメージとしては、
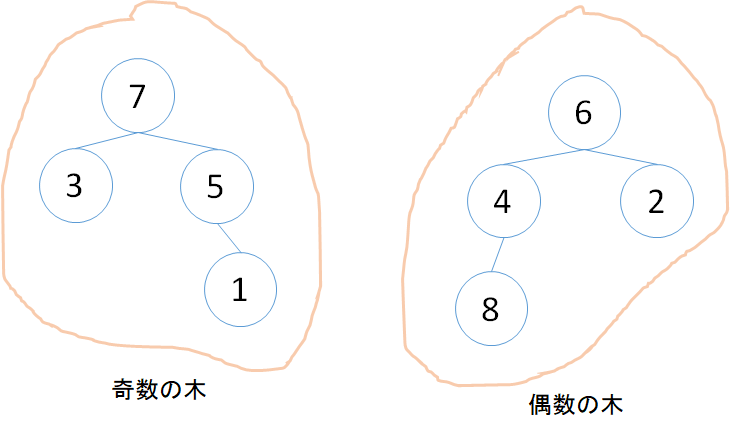
こんな感じです。Union-Find木がグループを管理するデータ構造であることがイメージできたかと思います。
Union-Find木の機能と実装
それではUnion-Find木の機能を紹介しながら、Pythonで実装していきます。
今回はクラスとして組んでいきます。
準備
何事も準備が肝心です。まずは、木の親要素を管理するリストparをつくります。
ここでpar[x]==xの場合には、そのノードが根であることを示します。
初期状態では一切グループ化されていないので、すべてのノードが根になりますね。
class UnionFind: def __init__(self, n): # 親要素のノード番号を格納。par[x] == xの時そのノードは根 self.par = [i for i in range(n+1)]
また、ノード番号とリストのインデックスを一致させるために長さ(N+1)のリストを作っています。
そして説明しやすさのために、ノード番号は1から始まることにしましょう。
例えば、[0, 1, 1]の時、1は根で、2の親が1であることを示します。(ノード番号0は存在しない)
検索(find)
Union-Find木の役割は、グループごとの管理です。裏を返せば、「ある2つの要素が同じグループに属するか判定する」という機能が必要になります。
では、何をもってある2つの要素が同じグループに属すると判定すればよいでしょうか。答えは単純で、ある2つの要素がそれぞれ属する木の根が同じかどうかをチェックすればよいですね。
つまり、親の親の親の・・・と根にたどり着くまで走査すればよいことがわかります。
これは再帰関数を用いて表現できます。
# 検索 def find(self, x): # 根ならその番号を返す if self.par[x] == x: return x # 根でないなら、親の要素で再検索 else: return self.find(self.par[x])
ただしこのままでは、同じ値を何度について何度も検索するときに手間がかかります。そこで、一度調べた値については根に繋ぎなおすことにしましょう。
さらに、親の親の・・・と調べ上げていく過程でそれぞれの根もわかるので、同様に根に繋ぎ変えてやります。
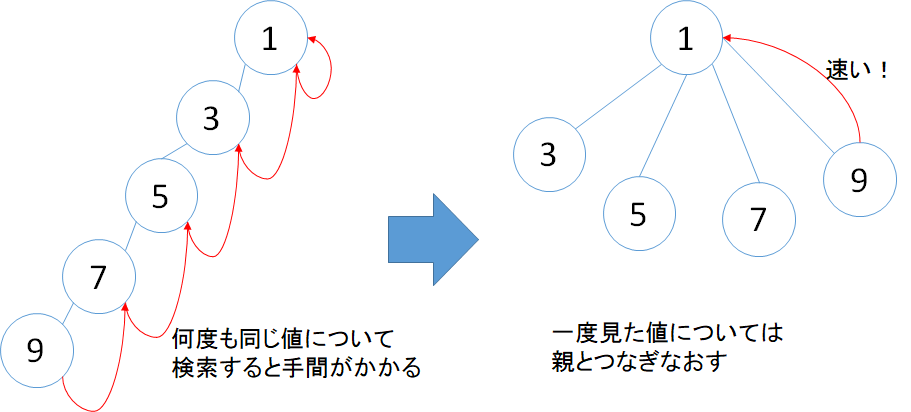
(2018/02/06追記:図では親と繋ぎなおすことになっていますが、正しくは根です)
これらの工夫はほんの1行追加するだけで、実装できます。
# 検索 # 根ならその番号を返す def find(self, x): if self.par[x] == x: return x else: # 走査していく過程で親を書き換える self.par[x] = self.find(self.par[x]) return self.par[x]
これである値の属するグループの根を検索する関数ができました。
これを用いて、ある2つの要素が同じグループに属するかを判定する関数を作ってみます。
# 同じ集合に属するか判定 def same_check(self, x, y): return self.find(x) == self.find(y)
併合(union)
次にあるグループとあるグループを1つのグループにまとめる、「併合(union)」を実装してみます。
先ほどのfind関数の実装例から、
- 木の高さは低いほうがよい
- 親要素の書き換えは少ないほうが良い
ことがわかるので、
「木の高さが低いほうの根から、高いほうの根へ辺を張る」ことで高速な併合を実現します。
そこで、木の高さを格納するリストrankをinitにてつくることにしましょう。 こちらも0を考慮し長さn+1のリストになります。
また根のrankが木の高さとなります。
def __init__(self, n): self.par = [i for i in range(n+1)] # 木の高さを格納する(初期状態では0) self.rank = [0] * (n+1)
あとは簡単で、ある値が含まれている根の木の高さを比較し、低いほうの根の親を高いほうの根にしてやるだけです。
仮に木の高さが同じだった場合には、片方の高さを+1してやることにします。
# 併合 def union(self, x, y): # 根を探す x = self.find(x) y = self.find(y) # 木の高さを比較し、低いほうから高いほうに辺を張る if self.rank[x] < self.rank[y]: self.par[x] = y else: self.par[y] = x # 木の高さが同じなら片方を1増やす if self.rank[x] == self.rank[y]: self.rank[x] += 1
完成形
できあがったUnion-Find木クラスは以下のようになります。
class UnionFind: def __init__(self, n): self.par = [i for i in range(n+1)] self.rank = [0] * (n+1) # 検索 def find(self, x): if self.par[x] == x: return x else: self.par[x] = self.find(self.par[x]) return self.par[x] # 併合 def union(self, x, y): x = self.find(x) y = self.find(y) if self.rank[x] < self.rank[y]: self.par[x] = y else: self.par[y] = x if self.rank[x] == self.rank[y]: self.rank[x] += 1 # 同じ集合に属するか判定 def same_check(self, x, y): return self.find(x) == self.find(y)
Union-Findに重みを付けてみる
at274.hatenablog.com 重み付きバージョン書きました!よかったらどうぞ!